My path to finding better Arduino random numbers, started with wanting a bit of code to pick winning raffle ticket numbers and display it on the I2C Display Add-on. I immediately noticed that what I thought would be random ticket numbers returned, turned out to be not so random after all: on tries 2, 3 and 5, the same ticket number appeared. I know better than to simply use random() to generate a number, because the internal algorithm produces a fixed sequence of numbers, and you have to seed it with some value to get true psuedo-random numbers. I had seeded it with an analogRead of A0, and yet the same values had popped up. I started pulling on that thread and this is the result.
Background
Bit Shifting
Bit Masking
I do have some caveats to make: I am not a mathematician, nor a cryptologist, number theorist, or pretty much anything that ends with “ist” (I am quite a few things that end with “er”). I can understand the barest surface of the theory behind random number generation true, psuedo or otherwise. Consider that I only went down this path because I thought it would be cooler to display raffle ticket numbers on a seven segment display than just picking the matching ticket out of a bag. That’s my starting point.
How Default Arduino Random Works
When you execute the random() command in your code, you are running something actually located in the wmath.cpp file, but that just does some checking to make sure the submitted values were formatted correctly, then passes it on to the stdlib.h file, which then uses the source code in the avr-libc standard libraries to do the heavy lifting. That chunk of avr-libc code comes precompiled with the Arduino IDE installation, so you can’t just search for the source on your machine to view it. As of this writing, the Arduino IDE uses avr-libc v2.0.0, which, if you really feel like it, can be downloaded here: http://download.savannah.gnu.org/releases/avr-libc/ and I’ve included the relevant source code at the bottom of this post for easy reference (and because it’s copyrighted, so want to give The Regents of the University of California their due).
I’ve culled out the relevant source code for our viewing here, and cleaned it up a bit to make it more legible.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
void setup() { Serial.begin(115200); long upperBound = 0; long lowerBound = 0; long seedValue = 0; seedValue = 1; for (uint8_t i = 0; i <= 9; i++) { if (seedValue == 0) seedValue = 123459876L; // Prevent the Seed Value from being zero upperBound = seedValue / 127773L; // Create an upper bound to prevent overflowing 31 bits lowerBound = seedValue % 127773L; // Create a lower bound to prevent overflowing 31 bits /* THIS IS WHERE THE "RANDOM" VALUE IS GENERATED. The calculation performed below is designed to generate a value that won't overflow and then the result is used to seed the next calculation. */ seedValue = 16807L * lowerBound - 2836L * upperBound; if (seedValue < 0) seedValue += 0x7fffffffL; // If seedValue is now negative for some reason, flip it to a positive value. /* RANDOM_MAX is defined in stdlib as 0x7FFFFFFF, 0x01 below where a signed long variable becomes negative This prevents overflow, because if seedValue is between 0 and RANDOM_MAX then seedValue modulo RANDOM_MAX will return seedValue. If it's too big, then the modulo of seedValue returns a much smaller number. */ uint32_t danValue = ((seedValue) % ((unsigned long)RANDOM_MAX + 1)); uint32_t avrValue = random(); Serial.print ("Dan Generated Random : 0x"); Serial.println (danValue, HEX); Serial.print ("AVRLIBC Generated Random : 0x"); Serial.println (avrValue, HEX); Serial.print ("Difference = "); Serial.println (danValue - avrValue); Serial.println (); } } void loop() { } |
There you go… that’s where random numbers are born in your Arduino: 16807 * someBound – 2836 * someOtherBound. Somehow I thought it would be more magical / intricate / byzantine than that, but it’s not, and that’s why it’s a psuedorandom number generator. The numbers aren’t random at all, just products of a publicly available formula. Good for repetitive testing, but crap for actually doing something as simple as picking raffle tickets.
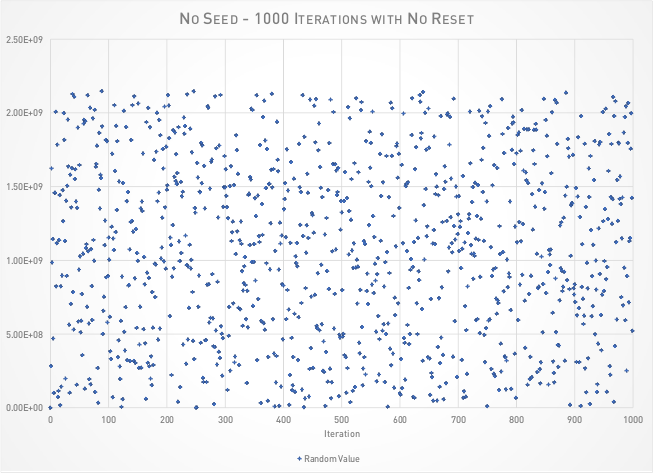
If you just run random() over and over and over again in your code, it may look like it’s giving you random values because the output doesn’t seem to repeat. The visual distribution (about the only way I have of categorizing this stuff, since I don’t have test software for randomness) is nice and… well… random… dispersed… unclumpy. There isn’t a visual pattern emerging after pumping out 1000 random values.
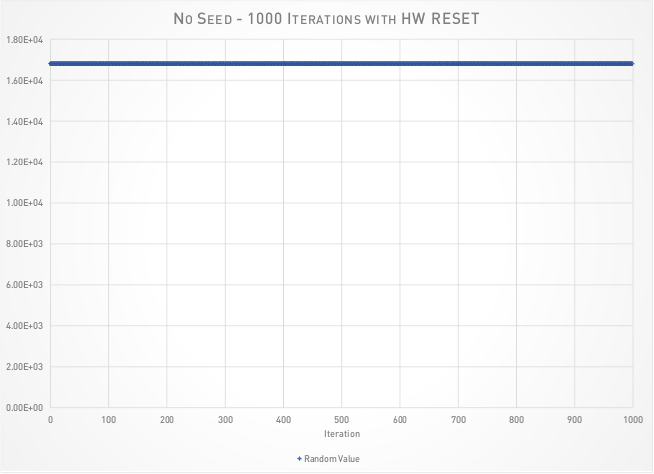
The problem shows up after reset. As a control, I reset the microcontroller 1000 times and grabbed the first value generated by random(). The results were as expected.
The Random Seed a.k.a. Why the Arduino Random Returns 16807
The reason that you get the same value over and over and over again is because on reset, the seed value, the value used as the input to the simple formula above, is the number 1. That result of the formula is then fed back as the next seed through the calculation, but it always starts at 1. Since the formula never changes, and the input is always 1, the output is always the result of 16807 * 1 % 127773 – 2836 * 1 / 127773. Plonk that into your calculator and you get: 16807. The perfectly flat line up there.
To help this, you can seed the formula with a different number, and get a different result out of the calculation using randomSeed(). It doesn’t change how the calculation works, just where you start in it. That is the whole point of the randomSeed function, to allow you to specify that starting point for the next go around through the formula.
I’ve created a spreadsheet that explores the original formula as described in the comments of the random function in the AVRLIBC standard library, and you can find that linked here: avr_stdlib_random.xlsx. After going through it a bunch, I kind of / sort of understand what’s going on with the exception of why they chose seven to the power of five. The idea is to be able to keep feeding the seed back in without overflowing the value of a signed long variable, but that 7^5 is baffling to me.
As I mention in the first paragraph, the method usually recommended is to seed the random calculation with the voltage level of a disconnected analog pin on the Arduino using analogRead(). That pin is in a “floating” state… you haven’t defined it’s pinMode or sent a digitalWrite high or low, so it starts off wherever transient electrons choose to drive it, but it’s definitely not 0V or 5V, it floats in between, so the value is constantly changing, if only slightly. But “slightly changing” is better than “the whole number 1”, which never changes.
Except, I discovered that analogRead(A0), at least in my environment with my bare UNO sitting on my desk at this temperature with these monitors and wireless mouse and keyboard and all the electronic whatnots and doodads sitting around, doesn’t really exhibit a tremendous amount of fluctuation, and the change it does demonstrate, is definitely predictable at least at the large scale view.
analogRead Alone is not your Random Solution
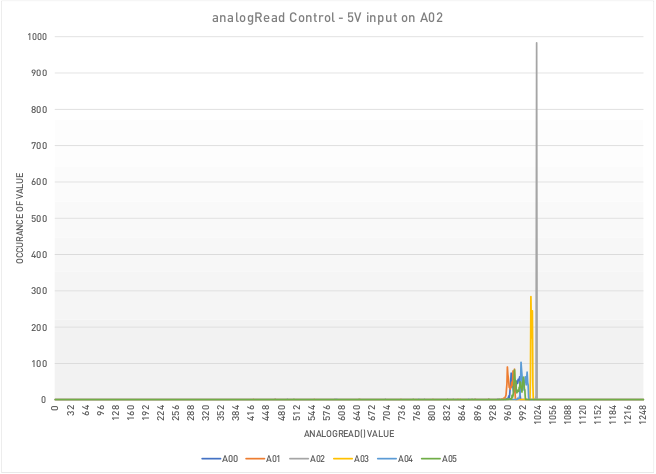
As a control, I tied Analog 02 to 5V, left the others floating and read the value of all the analog pins 1000 times. The following chart shows how many times each potential 10 bit value appeared in the results. As expected, A02 had nearly all 1000 values right at the maximum 1024 (0x3FF), with the others clustered around it as the transient voltage was spilling over to them.
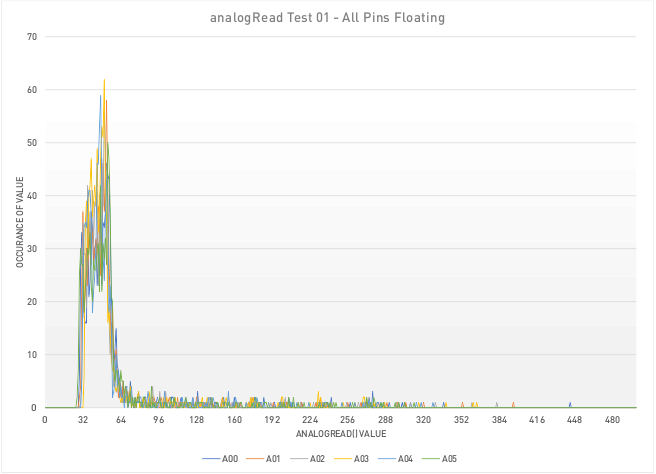
I then removed the connection to 5V so all the analog pins were now floating and reran the test again after powering the UNO fully off. Now, no values above 448 were returned, and all the pins were clustered down at the very low range of the scale. So they were floating above ground voltage, but not by very much. And out of 1000 reads, there were a significant number of duplicates returned for each pin.
Narrowing in on just Analog 00, I looked at it two ways: first to see how the values were distributed and secondly, how the values were changing over time. Again, out of 1000 reads the readings were clustered between the low values of 280 to 450, and the trend of how the values changed was surprising, a slowly decreasing wave of values, giving ample opportunity for duplicates to be returned. And if duplicates are returned, that’s just not very random, is it! Just to validate this, I reran that test 25 times, resetting the Arduino after each run, and the results showed a bit of a trend.
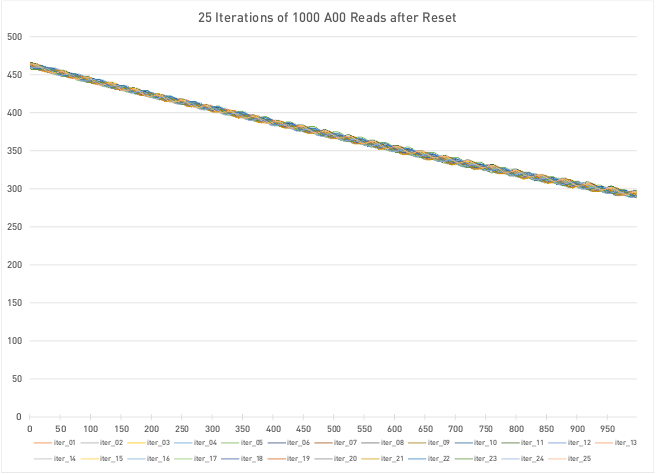
Simply reading the value of a floating analog pin and using that as your random seed just isn’t the answer! There isn’t sufficient variation!
Or is there…
The Significance of Bits
Looking at those graphs of A0 you can see that, while the voltage doesn’t change an awful lot, swinging back up on itself regularly, it is actually changing! So the trick then is to capture the part that changes the most and bend it to your will.
The array of bits that are returned from an analogRead represent buckets of voltage values. The least significant bit, the right most bit, represents a value of 0.0048V, while the most significant bit, the left most bit, represents a value of 2.500V. A full set of 1’s in all 10 bits results in a maximum ADC value of 1024, and with a 5V reference, that’s where the 0.0048 comes from: 5.0000 / 1024. Each bit position then, represents that 4.8mV multiplied by 2 ^ the bit position.
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| 2.50000 | 1.25000 | 0.62500 | 0.31250 | 0.15625 | 0.07813 | 0.03906 | 0.01953 | 0.00977 | 0.00488 |
So an ADC value of B0011111010 (0x0F6) would be
0 + 0 + 0.625 + 0.31250 + 0.15625 + 0.07813 + 0.03906 + 0 + 0.0097 + 0 = 1.22070V
The reason this is important, is that while the pin is sitting there gently wafting it’s way from somewhere north of 450 down to somewhere south of 300, the most significant bits won’t change very much, but the least significant bits are changing constantly. If you can capture enough of them over some length of time, you’ll get a much better random array of values that were fluctuating, and can feed THAT in as the random seed.
This had to be tested, so I captured 1000 values of the least signficant bit of A00, and did that 50 times. The question was, how random was it. My thinking was as follows: since we’re only capturing a single bit, 0 or 1, that’s essentially a coin flip. If you flip a coin 50 times, you would expect somewhere around 25 heads and 25 tails. A statistician would be able to tell you likelihoods and probabilities, but I’m just running on the simplest premise… should be a 50/50 split between results if there isn’t a thumb on the scale.
I took each analogRead result and added it together to result of each subsequent run of the test: add all the first returned values together, add all the second returned values together, etc. If the results are really random, really coin flips, you would expect each sum to wind up at 25. It’s okay to get to 25 through any combination of 1’s and 0’s as they pop up, but ultimately, you want to see a large cluster of returns sitting right at 25, with some noise to either side that the untrained eye can look at and go, “yeah, I guess that makes sense.” Sure enough…
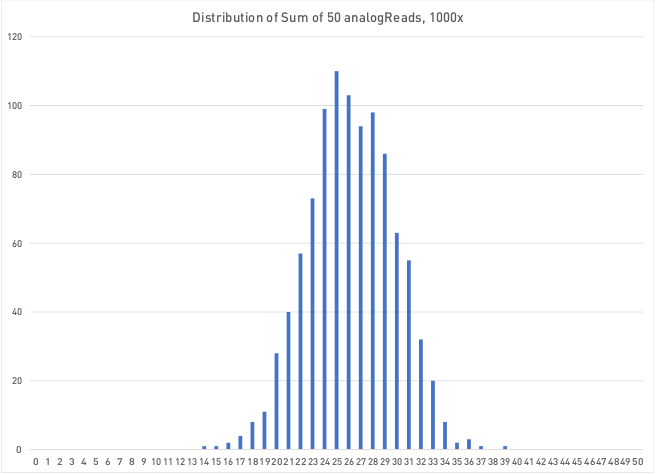
When you look at the summed value over time, it’s a nice jangly mess, again, clustered around 25. That means regardless of how long you wait to sample the floating value (at least in the first second or so after startup), you stand a good chance of that 0 or 1 being random.
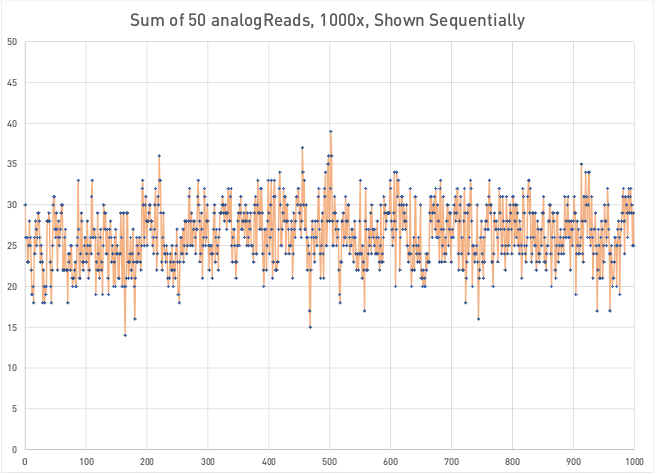
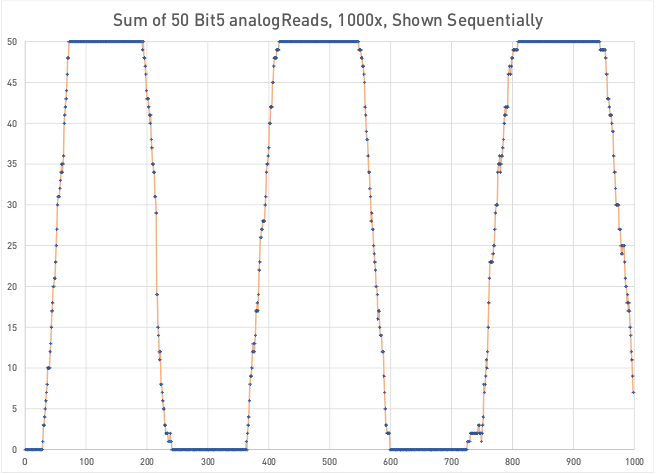
Just to make sure I wasn’t fooling myself, I reran the test, but sampled BIT 5 instead of the least significant bit. That meant there would have to be a voltage change of 15.6mV in order for that bit to change, instead of 4.8mV. The result shows that the values were clustered around 0 and 50, meaning all 50 buckets had either zeros or ones in them most of the time: far from random.
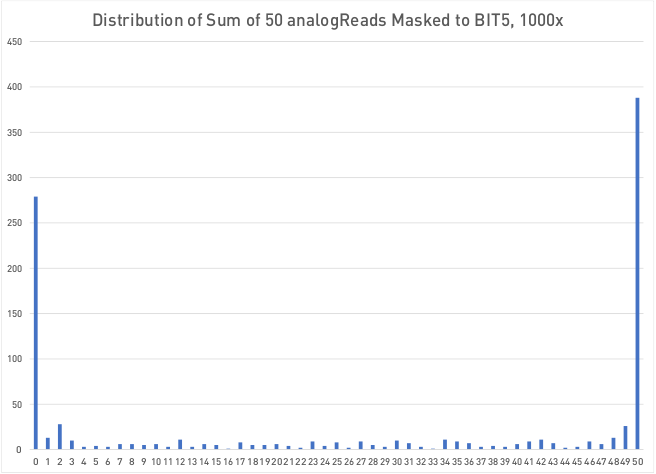
The result over time bore out that fact: over time, there are long stretches where repeatedly reading that bit would only ever get a one or only ever get a zero.
A Better Way to Seed Random
Here’s what I came up with, and I’ll tell you right now there are far better ways to generate random numbers: The Entropy Library and the BLOC97 Algorithm, and I’ll cover those in another tutorial. What I present here, while thoroughly untested against DIEHARD or any other proofs of randomness, is at least sufficient to pick a raffle ticket, or simulate rolling dice, and be pretty confident that you’re not going to duplicate yourself and disappoint your meetup attendees or piss off a party of adventurers. I know it’s not cryptographicologicialisticly sound, so no need to email me to let me know that. (although if you want to email me and explain why seven to the power of five is so prevelant in the AVR-LIBC formula above, go ahead!). But it’s easy to understand without having to know what WATCHDOG CLOCK JITTER is.
Enough preamble. We’ve got seeds to plant.
I read somewhere during my research for this, I think it was in the documentation of the BLOC97 Algorithm, that guessing the result of a single coin flip is easy, but guessing the sequence of a stack of coins is really hard. So what we need to do is flip the coin as many times as possible, as quickly as possible, stacking each coin on the next in a useful way to build that “really hard to guess” value. The coins (in this tortured analogy I can’t seem to let go of) are the least significant bits of the analogRead values of the pins, and they are flipping constantly while the pin voltage is floating. The stack of coins we’re going to make will be an unsigned 32bit value we’ll manufacture and then use to seed the random formula.
There are six analog pins to work with, and each one is able to pump out values from the moment your code enters SETUP. In some cases, you may have stuff connected to several of the pins, like the I2C pins for example, robbing you of floating voltages at those positions. Fortunately, you only need one free analog pin for this to work. Ideally you’d want that pin as far away from any connected pins as possible. Just spit a couple hundred seed values to the serial plotter in the Arduino IDE, and look for anything that resembles a pattern. If not, you’re probably good to go, but if so, then you’ll want to use BLOC97 or Entropy instead. I mean, you probably should use those instead anyway.
So, now that I’m done telling you to use something else, go ahead and pick your analog pin of choice, and create a constant for it in the declarations area called “seedPin”.
|
1 |
const uint8_t seedPin = A0; |
Next is the actual function that creates our seed value — our stack of flipped coins. All it really does is grab 32 least significant bits, and shuffles them into the spaces of a 32 bit value using bit shifting. Let’s look at it from the middle out.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
uint32_t generateRandomSeed() { uint8_t seedBitValue = 0; uint8_t seedByteValue = 0; uint32_t seedWordValue = 0; for (uint8_t wordShift = 0; wordShift < 4; wordShift++) // 4 bytes in a 32 bit word { for (uint8_t byteShift = 0; byteShift < 8; byteShift++) // 8 bits in a byte { for (uint8_t bitSum = 0; bitSum <= 8; bitSum++) // 8 samples of analog pin { seedBitValue = seedBitValue + (analogRead(seedPin) & 0x01); // Flip the coin eight times, adding the results together } delay(1); // Delay a single millisecond to allow the pin to fluctuate seedByteValue = seedByteValue | ((seedBitValue & 0x01) << byteShift); // Build a stack of eight flipped coins seedBitValue = 0; // Clear out the previous coin value } seedWordValue = seedWordValue | (uint32_t)seedByteValue << (8 * wordShift); // Build a stack of four sets of 8 coins (shifting right creates a larger number so cast to 32bit) seedByteValue = 0; // Clear out the previous stack value } return (seedWordValue); } |
We begin by flipping our coin eight times, adding the results together: the more times you flip the coin, the harder it is to guess. Then we take that resulting value and use only it’s least significant bit… the LSB of the sum of eight LSBs… that’s one well flipped coin.
Now we start to build stacks of eight coins using those bits. Each bit generated is shifted over by “byteShift” amount to the next available bit position until all 8 bits of the byte are full… we add a coin to the stack then flip another 8 of them until our stack of 8 coins is finished.
Once we’ve got our stack of eight coins, we use it to build four sets of eight coin stacks. When our byte is filled, we add it to the word value by shifting it over “wordShift” amount to the next available open byte… we stack the most recent 8 coins on top of whatever stack was already there until we have 32 coins. The distribution of values of the 32bit value created looks pretty random to me.
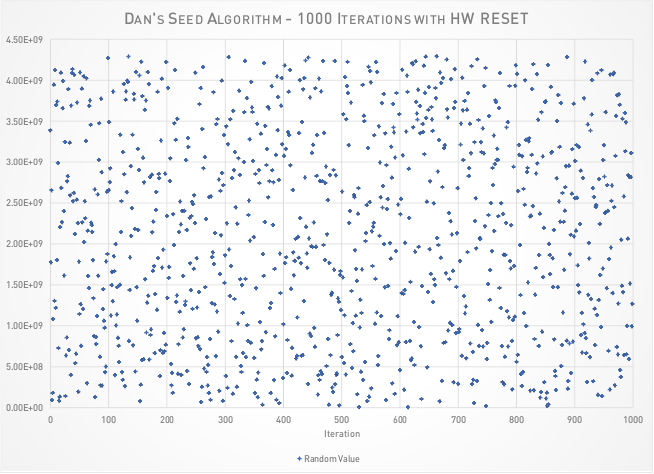
When we’re done, we’ve got a stack of 32 coins, representing 256 individual coin flips that were all based on whether a voltage had changed by more than 0.0048 volts. It’s not particularly fast at 64ms, but is pretty thorough. Considering that you’ll most likely just seed your random function once using this, it should be more than sufficient for most things that don’t involve having all the analog pins in use, or financial transactions. If timing isn’t particularly critical for you, just use this as your random value as well, works pretty alright for that. I ran a bunch of tests using A0 as the seedPin, with the I2C and SPI Education Shield connected, and the I2C Display plugged in as well, which means A0 and A1 where the only pins not in use, and the results were fine.
As mentioned above, here is the actual AVR-LIBC source code for the random function…
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 |
/*- * Copyright (c) 1990, 1993 * The Regents of the University of California. All rights reserved. * * Redistribution and use in source and binary forms, with or without * modification, are permitted provided that the following conditions * are met: * 1. Redistributions of source code must retain the above copyright * notice, this list of conditions and the following disclaimer. * 2. Redistributions in binary form must reproduce the above copyright * notice, this list of conditions and the following disclaimer in the * documentation and/or other materials provided with the distribution. * 3. Neither the name of the University nor the names of its contributors * may be used to endorse or promote products derived from this software * without specific prior written permission. * * THIS SOFTWARE IS PROVIDED BY THE REGENTS AND CONTRIBUTORS ``AS IS'' AND * ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE * IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE * ARE DISCLAIMED. IN NO EVENT SHALL THE REGENTS OR CONTRIBUTORS BE LIABLE * FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL * DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS * OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) * HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT * LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY * OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF * SUCH DAMAGE. * * Posix rand_r function added May 1999 by Wes Peters <wes@softweyr.com>. * * $Id: random.c 1944 2009-04-01 23:12:20Z arcanum $ */ /* * From: static char sccsid[] = "@(#)rand.c 8.1 (Berkeley) 6/14/93"; */ #include #include "sectionname.h" ATTRIBUTE_CLIB_SECTION static long do_random(unsigned long *ctx) { /* * Compute x = (7^5 * x) mod (2^31 - 1) * wihout overflowing 31 bits: * (2^31 - 1) = 127773 * (7^5) + 2836 * From "Random number generators: good ones are hard to find", * Park and Miller, Communications of the ACM, vol. 31, no. 10, * October 1988, p. 1195. */ long hi, lo, x; x = *ctx; /* Can't be initialized with 0, so use another value. */ if (x == 0) x = 123459876L; hi = x / 127773L; lo = x % 127773L; x = 16807L * lo - 2836L * hi; if (x < 0) x += 0x7fffffffL; return ((*ctx = x) % ((unsigned long)RANDOM_MAX + 1)); } ATTRIBUTE_CLIB_SECTION long random_r(unsigned long *ctx) { return do_random(ctx); } static unsigned long next = 1; ATTRIBUTE_CLIB_SECTION long random(void) { return do_random(&next); } ATTRIBUTE_CLIB_SECTION void srandom(unsigned long seed) { next = seed; } |





