There’s one last topic to cover in our discussion of number conversions. So far, all we’ve looked at has been manipulating positive numbers, or “unsigned” values which are always positive. However there will be times you need to deal with negative values. This module covers a common way of expressing negative values called “two’s complement”.
Objectives
- Understand where the sign bit is located in a two’s complement value.
- Be able to convert a value to and from decimal and two’s complement binary.
Background
Two’s Complement Wikipedia Page
Schematic
There is no schematic associated with this module.
Setup
There is no setup required for this module.
Two’s Complement Values
When we see a byte value spit at us from a piece of digital electronics, we see something like B00101101 and after doing some general conversion, that value translates to 45 in decimal. In the number conversion sections we did that left, right, sideways and upside down again and again. However, it all relates to positive numbers only. But if your temperature sensor wants to tell you the temperature in your freezer, what value does it send you, when all it can send is a 1 or a 0?
The solution to this is called two’s complement. The official description of two’s complement on Wikipedia is…
The two’s complement of an N-bit number is defined as the complement with respect to 2N
… and if you know what that means, then you’re a far greater person than I. It makes no sense to me. However, here’s how I’ve always understood the mechanics of two’s complement.
Take a standard 8-bit number as an example: Bxxxxxxxx. In regular unsigned notation, the minimum value of this is 0 and the maximum value, if you fill it up with ones, is 255. In two’s complement, the most significant bit becomes the sign indicator, and the rest of the bits still represent what you’ve come to know and love. However, the way you interpret the value is by taking the number you know and love, and adding it to -128. That becomes the final value.
Again… like I said… it’s mechanics. I’m not sure why it works… I just know it works.
I’m going to try to be consistent in this module, but talking about adding and subtracting negative and positive numbers can be a little confusing. Interpret anything I say absolutely literally: “add the negative value to 128”, means exactly that mathematically “-x + 128”.
So, let’s take our 8-bit example and add some values to it. Let’s start with B01110011. Now doing our regular conversion on it, we realize that it has a decimal equivalent of 115.

Let’s modify it now by adding a one in the most significant bit, B11110011. Through the standard conversion, we would obtain a decimal value of 243. However, since this is two’s complement, we know that this is a negative number, the left most bit is 1, so we determine the remaining seven bits and add that to -128.

Another example: let’s start with B00000011.

Now we change it to B10000011 and in two’s complement we now have a negative number.

Convert the two’s complement value B10011001 to decimal… (click here for a description of the solution)
Hover to read answer
Convert the two’s complement value B11111110 to decimal… (click here for a description of the solution)
Hover to read answer
Converting negative decimals to two’s complement
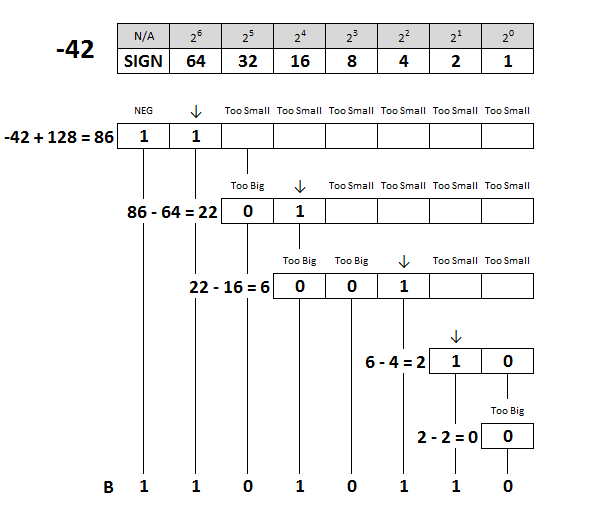
In two’s complement, converting a positive decimal is the same as always, however converting a negative decimal involves taking your negative decimal, adding it to 128 and converting the result to binary, while remembering to correctly set the sign bit.
So to convert -42, we add that to 128 and get 86. That is then converted to binary, with the MSB set to 1 to indicate a negative number is being represented.
Convert the decimal value -47 to two’s complement notation… (click here for a description of the solution)






