Generally, because I’ve been doing this so long, I can do 8 bit values in my head pretty fast (in the morning… post coffee… pre-lunch-food-coma) but even still, when I’m working down at the bit level, I always have the “Calc” application open in Windows, set to the “Programmer” interface, because it never makes mistakes, and has no problem with 32 bit values. A really simple alternative to that is MathIsFun Binary to Decimal to Hex converter web page. I am also not above writing this out on paper too. Sometimes it will only make sense to me when I see it on graph paper. If that’s what it takes, embrace it!
I’m going to stick to converting 8 bit numbers because if you can understand that, larger values are well within your grasp, but you’ll wind up using a converter anyway unless you get to the point where you do this day in, day out. Working with 8 bit binary numbers means possible decimal values from 0 to 255, and since I used 42 in all the number system examples, let’s convert that.
Decimal to Binary Conversion
The method I learned is very mechanical; more pattern matching than math. Let’s call it the Price Is Right System.
Step One: Look at the decimal number and find the position in the binary number system closest to that value without going over. That binary position gets a one in it, and any positions to the left get zeros.
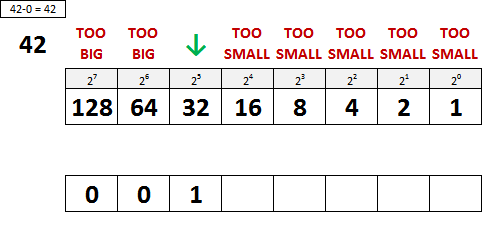
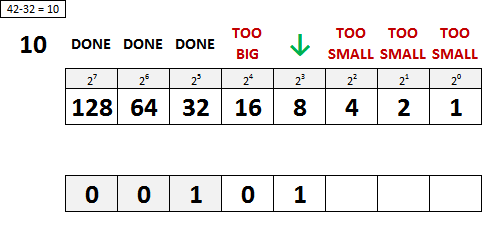
Step Two: Subtract the value of that binary position, in this case 32, from your original decimal value, in this case 42 … 42 – 32 = 10.
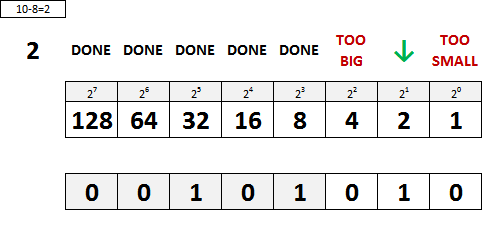
Step Three: Basically Step One again, find the value that is as close as you can get to the remaining value of your decimal without going over. That position gets a one, and any empty positions to the left get a 0.
Repeat Eventually, you will find yourself with a remaining value, after the subtraction, of 0. That means you’re done. Any empty spots to the right should now be filled in with zeros as well.
Convert the Decimal 208 to Binary… here is another example, this time without all my chatter and condensed into a slide show.
[masterslider id=42]Here are a few practice problems…
Convert the Decimal 54 to Binary… (click here for a description of the solution)
Hover to read answer
Convert the Decimal 231 to Binary… (click here for a description of the solution)
Hover to read answer
Convert the Decimal 7 to Binary… (click here for a description of the solution)
Hover to read answer
Remember, you’re only learning this so that you can look into the code you’re writing and understand what’s going on. You’re not going to start balancing your check book this way, so don’t think twice about using automated tools to help you with this, once you understand how to do the conversion manually.
Binary to Decimal Conversion
I find this significantly easier to do than converting from decimal to binary. All I do is write out the binary value, with the position value above it, then add up the position values with ones in their location. To be fair, I have done this so many times that I can rattle off powers of 2 very quickly, so scribbling down 1, 2, 4, 8, 16, 32, 64, 128 is fast (and yes, I do it in my head most of the time). You’ll get there too with practice.
Convert B11010100 to Decimal…

Convert B00110101 to Decimal…

Here are a few practice problems…
Convert B00010100 to Decimal… (click here for a description of the solution)
Hover to read answer
Convert B01000100 to Decimal… (click here for a description of the solution)
Hover to read answer
Convert B11011110 to Decimal… (click here for a description of the solution)